NumPy Exercises#

import numpy as np

np.zeros(3, dtype=int)

np.ones((2, 3))

np.empty((3, 2, 3), dtype=float)

Exercise 1#

Create a 3D array of integers, 2 x 2 x 3, filled with the number 10

A = ...

Exercise 2#

Create a 2D array of integers, 5 x 6, where each item is the product of its row and column:

\[ A_{i, j} = i \cdot j ; \text{where } i \in [1,5], j \in [1,6] \]
A = ...

Suggestion: Use for example np.ndindex

Write help(np.ndindex) to see its docstring.

Exercise 3#

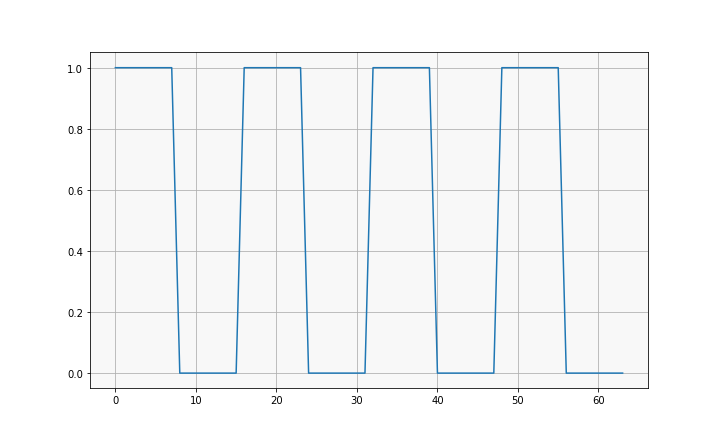
Make a square wave \(u^0\):

  • length = 64

  • where every 8 elements is either 0 or 1

squarewave

Bonus: 2D!

  • 64 x 64, floats

  • where every 8 rows and columns is either 1 or 0

%matplotlib inline
import matplotlib.pyplot as plt

u0 = ...

Physics!#

The heat equation is often used for blurring:

(1)#\[\begin{align} \frac{\partial u}{\partial t} &= - \frac{\partial^2 u}{\partial x^2} &&\quad \text{ for } x \in I, \, t \in T. \end{align}\]

We use our square wave as initial solution: $\( u = u^0(x) \quad \text{ at } t=0, \)\( and fix the value of \)u$ at the left and right endpoints:

(2)#\[\begin{align} u &= 1 &&\quad \text{ at } x=0, \\ u &= 0 &&\quad \text{ at } x=N.\\ \end{align}\]

Take \(I = (0, N)\) and \(T = (0,M)\).

We now \(discretize\) the heat equation as follows $$

(3)#\[\begin{align} u_i^{n+1} & = u_i^{n} + \frac{1}{4} \left( u_{i-1}^n - 2 u_{i}^n + u_{i+1}^n \right) ; i \in [1,N-1] \\ u_0^{n+1} & = u_0^n \\ u_N^{n+1} & = u_N^n \end{align}\]

$\( where \)u_i^n\( means \)u\( at \)x_i=i\( and \)t=n$

Exercise 4:#

Implement a number of steps of the heat equation.

def heat(u0, time_steps=1):
    
    u_n = u0 # u_n is the solution at the previous time step
             # we initialize it as u0
    
    for i in range(time_steps):
        
        # Apply our discretization!
        u_n1[...] = ....
        
        # Assign u_n1 as previous solution
        # and proceed to next time step
        u_n = u_n1
    return u_n1

# Plot the solution
x = range(64)
plt.plot(x, u, label="square")
plt.plot(x, heat(u), label="heat(1)")
plt.plot(x, heat(u, 10), label="heat(10)")
plt.plot(x, heat(u, 50), label="heat(50)")
plt.legend(loc=0)

Suggestions:

  • Use a for loop to iterate through range(N). You can then access elements to the left as u_n[i-1] and to the right as u_n[i+1]

  • Splice the arrays together. For example, u_n[1:-1] will return all elements of u_n except the left and right endpoints

Exercise 4 bonus:#

In two dimensions, the stencil reads $$

(4)#\[\begin{align} u_{i,j}^{n+1} & = u_{i,j}^{n} + \frac{1}{4} \left( u_{i-1,j} + u_{i,j-1} - 4 u_{i,j} + u_{i+1,j} + u_{i,j+1} \right) ; i,j \in [1,N-1] \\ u_{0,j}^{n+1} & = u_{0,j}^n \\ u_{N,j}^{n+1} & = u_{N,j}^n \\ u_{i,0}^{n+1} & = u_{i,0}^n \\ u_{i,N}^{n+1} & = u_{i,N}^n \end{align}\]

$$

Implement the discretized heat equation in 2D.

Break??#

Exercise 5#

The dot product \(u \cdot v\) for vectors is defined as the cumulative sum of the elementwise product of \(u\) and \(v\):

\[ u \cdot v = \sum_{i=0}^N u_i v_i \]

Part 1: implement the dot product for any two Python iterables

def dot(u, v):
    result = 0

    ...

    return result

N = 100
u = np.arange(N)
v = np.arange(N)

dot(u, v)

Part 2: Measure how long it takes to call your function for iterables of sizes 1000 - 1,000,000

Suggestion: Use tic and toc as below

import time

tic = time.perf_counter()
time.sleep(0.1)
toc = time.perf_counter()
duration = toc - tic
print(f"sleep(0.1) took {duration:.4f}s")

for N in [1000, 10_000, 100_000, 1_000_000]:
    ...

    r = dot(u, v)

    ...

    print(f"N={N:8}, {1000 * (toc-tic):8.2f}ms")

Numpy has its own builtin dot function:

np.dot(u, v)

This is also called via the matrix multiplication operator @:

u @ v

How does numpy’s dot function perform?

for N in [1000, 10_000, 100_000, 1_000_000]:
    ...
    u = np.arange(N)
    v = np.arange(N)
    r = np.dot(u, v)
    ...
    print(f"N={N:8}, {1000 * (toc-tic):8.2f}ms")

Plotting#

%matplotlib inline
import matplotlib.pyplot as plt

For basic plots, plt.plot takes an x list or array and a y list or array and plots them on a linear scale:

For certain kinds of data, a linear scale isn’t a great fit:

x = [1, 10, 100, 1_000, 10_000, 100_000]
x_squared = np.array(x) ** 2

plt.subplot(1, 2, 1)
plt.plot(x, x_squared, "-o")
plt.title("  x^2 with linear plot")

plt.subplot(1, 2, 2)
plt.loglog(x, x_squared, "-o")
plt.title("  x^2 with loglog plot")

The slope on a linear scale is \(\frac{y}{x}\). The slope on a log-log scale is \(\frac{log(y)}{log(x)}\).

\[\begin{split} \begin{align} y &= x ^ 2 \\ \frac{y}{x} & = x \\ log(y) & = log(x^2) = 2 log(x) \\ \frac{log(y)}{log(x)} &= 2 \text{ (log-log slope) } \end{align} \end{split}\]

Exercise 6#

collect timings for your dot product and numpy’s dot for a range of lengths up to \(\sim10^6\), and plot:

  1. a separate line for each implementation on one plot, and

  2. a single line showing numpy performance relative to yours

Think about what axis scale is most appropriate for your data

my_times = []
numpy_times = []
relative_performance = []

Ns = [1000, 10_000, 100_000, 1_000_000]

for N in Ns:
    u = np.arange(N)
    v = np.arange(N)

    ...

plt.loglog(Ns, numpy_times, label="np")
plt.loglog(Ns, my_times, label="mine")
plt.legend()
plt.xlabel("N")
plt.ylabel("time")